Aqui tratamos de grafos que deixam de ser conexos quando perdem uma de suas arestas. Ela se restringe a grafos, pois os conceitos discutidos não fazem sentido em digrafos não-simétricos.
Pontes em grafos
Uma aresta de um grafo é uma ponte (= bridge = separation edge) se ela é a única aresta que atravessa algum corte do grafo. [Pontes são também conhecidas com arestas de corte, mas nós não vamos usar essa terminologia.]
Em outras palavras, uma ponte é uma aresta cuja remoção aumenta o número de componentes do grafo.
Problema: Encontrar as pontes de um grafo dado.
Poderíamos aplicar cegamente a definição de ponte para resolver o problema, mas é possível fazer coisa melhor.
Pontes e busca em profundidade
É possível encontrar as pontes de um grafo de maneira muito eficiente. O ponto de partida é o seguinte fato básico: em qualquer grafo, uma aresta é uma ponte se e somente se não faz parte de um ciclo não-trivial. (Em outras palavras, toda aresta é de um e apenas um de dois tipos: ou ela é uma ponte ou pertence a um ciclo não-trivial.)
Se fizermos uma busca em profundidade no grafo, um dos dois arcos que constituem qualquer ponte será necessariamente um arco de arborescência (por que?). Agora observe a seguinte
Propriedade: Em qualquer busca em profundidade, um arco v-w da floresta DFS faz parte (juntamente com w-v) de uma ponte se e somente se não existe arco de retorno que ligue um descendente de w a um ancestral de v.
(Os descendentes e ancestrais de que trata a propriedade não são necessariamente próprios.) Para tirar proveito dessa propriedade, vamos calcular, para cada vértice v, o menor número de pré-ordem (= lowest preorder number) que pode ser alcançado a partir de v. Esse número será denotado por
menorpre[v].
Explico melhor: Digamos, só para efeito desta explicação, que um caminho é interessante se
- começa em v,
- "desce" pela arborescência de busca em profundidade,
- e finalmente percorre no máximo um arco de retorno.
(Por exemplo, todo caminho de comprimento 0 que começa em v é interessante. Outro exemplo: um caminho de comprimento 1 que começa em v e percorre um só arco de retorno é interessante.) Digamos que o valor de um caminho interessante é lbl[z], sendo z o último vértice do caminho. Então low[v] é, por definição, o valor de um caminho interessante de valor mínimo.
É claro que menorpre[v] ≤ ordemvisit[v] para todo vértice v. Digo mais: para todo arco v-w do grafo,
- se v-w é um arco de arborescência (e portanto v é pai de w) então menorpre[v] ≤ menorpre[w];
- se v-w é uma arco de retorno (e portanto ordemvisit[v] > ordemvisit[w]) então menorpre[v] ≤ ordemvisit[w].
Algoritmo das pontes
A propriedade acima pode ser reformulada assim: em qualquer floresta de busca em profundidade de um grafo, um arco de arborescência v-w faz parte de uma ponte se e somente se menorpre[w] == ordemvisit[w].
O teste "if (p != pai[v])" garante que v-w é um arco de retorno (e não um arco-pai).
A função todasPontes é linear: ela consome tempo proporcional a V+E. A variante dessa função para matrizes de adjacência consome tempo proporcional a V².
Aresta-biconexão
Um grafo é aresta-biconexo (= edge-connected) ou 2-aresta-conexo se for conexo e não tiver pontes. Portanto, é preciso remover pelo menos duas arestas de um grafo aresta-biconexo para que ele deixe de ser conexo.
Fato básico importante: Um grafo é aresta-biconexo se e somente se, para cada par (s,t) de seus vértices, existem (pelo menos) dois caminhos de s a t sem arestas em comum.
Uma componente aresta-biconexa (= edge-connected component) de um grafo é qualquer componente do grafo que se obtém depois que todas as pontes são removidas.
Exercícios para Fixação
1. Mostre que todas as arestas de qualquer floresta são pontes. A recíproca é verdadeira?
2. Escreva uma função que calcule menorpre[v] para cada vértice v de um grafo dado.
3. Diga o que a função ponte faz.
4. Execute a função todasPontes para encontrar as pontos dos grafos da figura abaixo:
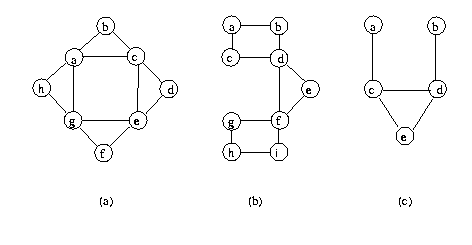
5. Escreva uma função que receba um grafo G e devolva 1 se o grafo é aresta-biconexo e devolva 0 em caso contrário. (Sugestão: modifique os códigos já apresentados nesta aula)
6. Qual o número mínimo de arestas de um grafo aresta-biconexo que tem V vértices?
Referência: IME
Pontes em grafos
Uma aresta de um grafo é uma ponte (= bridge = separation edge) se ela é a única aresta que atravessa algum corte do grafo. [Pontes são também conhecidas com arestas de corte, mas nós não vamos usar essa terminologia.]
Em outras palavras, uma ponte é uma aresta cuja remoção aumenta o número de componentes do grafo.
Problema: Encontrar as pontes de um grafo dado.
Poderíamos aplicar cegamente a definição de ponte para resolver o problema, mas é possível fazer coisa melhor.
Pontes e busca em profundidade
É possível encontrar as pontes de um grafo de maneira muito eficiente. O ponto de partida é o seguinte fato básico: em qualquer grafo, uma aresta é uma ponte se e somente se não faz parte de um ciclo não-trivial. (Em outras palavras, toda aresta é de um e apenas um de dois tipos: ou ela é uma ponte ou pertence a um ciclo não-trivial.)
Se fizermos uma busca em profundidade no grafo, um dos dois arcos que constituem qualquer ponte será necessariamente um arco de arborescência (por que?). Agora observe a seguinte
Propriedade: Em qualquer busca em profundidade, um arco v-w da floresta DFS faz parte (juntamente com w-v) de uma ponte se e somente se não existe arco de retorno que ligue um descendente de w a um ancestral de v.
(Os descendentes e ancestrais de que trata a propriedade não são necessariamente próprios.) Para tirar proveito dessa propriedade, vamos calcular, para cada vértice v, o menor número de pré-ordem (= lowest preorder number) que pode ser alcançado a partir de v. Esse número será denotado por
menorpre[v].
Explico melhor: Digamos, só para efeito desta explicação, que um caminho é interessante se
- começa em v,
- "desce" pela arborescência de busca em profundidade,
- e finalmente percorre no máximo um arco de retorno.
(Por exemplo, todo caminho de comprimento 0 que começa em v é interessante. Outro exemplo: um caminho de comprimento 1 que começa em v e percorre um só arco de retorno é interessante.) Digamos que o valor de um caminho interessante é lbl[z], sendo z o último vértice do caminho. Então low[v] é, por definição, o valor de um caminho interessante de valor mínimo.
É claro que menorpre[v] ≤ ordemvisit[v] para todo vértice v. Digo mais: para todo arco v-w do grafo,
- se v-w é um arco de arborescência (e portanto v é pai de w) então menorpre[v] ≤ menorpre[w];
- se v-w é uma arco de retorno (e portanto ordemvisit[v] > ordemvisit[w]) então menorpre[v] ≤ ordemvisit[w].
Algoritmo das pontes
A propriedade acima pode ser reformulada assim: em qualquer floresta de busca em profundidade de um grafo, um arco de arborescência v-w faz parte de uma ponte se e somente se menorpre[w] == ordemvisit[w].
#define MAXV 100 //número máximo de vértices
int G[MAXV][MAXV]; //grafo representado por matriz de adjacência
int ordemvisit[MAXV]; //marca a ordem de visitação dos vértices
int menorpre[MAXV]; //menor o menor número de pré-ordem que pode ser alcançado a partir de v
int pai[MAXV]; //vetor de pai, pai de X é pai[X]
int n; //número de vértices neste grafo
int count; //contador
int countpontes; //contador de pontes
//A função abaixo calcula o número de pontos, countpontes, do grafo G e imprime todas as pontes
void todasPontes(){
int v;
for( v = 0 ; v < n ; ++v ){
ordemvisit[v] = -1;
}
for( v = 0 ; v < n ; ++v ){
if(ordemvisit[v] == -1){
pai[v] = v;
ponte(v);
}
}
}
void ponte(int v){
int p, v;
ordemvisit[v] = count++;
menorpre[v] = ordemvisit[v];
for( p = 0 ; p < n ; ++p ){
if(ordemvisit[p] == -1){
pai[p] = v;
ponte(p);
if ( menorpre[v] > menorpre[p])
menorpre[v] = menorpre[p];
if ( menorpre[p] == ordemvisit[p]){
countpontes++;
printf("%d-%d\n", v, p);
}
}
else if( p != pai[v] && menorpre[v] > ordemvisit[p] )
menorpre[v] = ordemvisit[p];
}
}O teste "if (p != pai[v])" garante que v-w é um arco de retorno (e não um arco-pai).
A função todasPontes é linear: ela consome tempo proporcional a V+E. A variante dessa função para matrizes de adjacência consome tempo proporcional a V².
Aresta-biconexão
Um grafo é aresta-biconexo (= edge-connected) ou 2-aresta-conexo se for conexo e não tiver pontes. Portanto, é preciso remover pelo menos duas arestas de um grafo aresta-biconexo para que ele deixe de ser conexo.
Fato básico importante: Um grafo é aresta-biconexo se e somente se, para cada par (s,t) de seus vértices, existem (pelo menos) dois caminhos de s a t sem arestas em comum.
Uma componente aresta-biconexa (= edge-connected component) de um grafo é qualquer componente do grafo que se obtém depois que todas as pontes são removidas.
Exercícios para Fixação
1. Mostre que todas as arestas de qualquer floresta são pontes. A recíproca é verdadeira?
2. Escreva uma função que calcule menorpre[v] para cada vértice v de um grafo dado.
3. Diga o que a função ponte faz.
4. Execute a função todasPontes para encontrar as pontos dos grafos da figura abaixo:

5. Escreva uma função que receba um grafo G e devolva 1 se o grafo é aresta-biconexo e devolva 0 em caso contrário. (Sugestão: modifique os códigos já apresentados nesta aula)
6. Qual o número mínimo de arestas de um grafo aresta-biconexo que tem V vértices?
Referência: IME


